$
\def\RR{{\text{I}\!\text{R}}} \def\NN{{\text{I}\!\text{N}}} \newcommand{\ZZ}{\mbox{Z}\!\!\mbox{Z}}
\def\CC{{\cal C}} \def\QQ{{\text{Q}\!\!\!\scriptsize^|\:\:}}
\def\dint{\mathop{\int\!\!\int}} \def\tint{\mathop{\int\!\!\int\!\!\int}}
\def\rot{\hbox{rot\hskip2truept }}
\def\div{\hbox{div\hskip2truept }}
\def\grad{\hbox{grad\hskip2truept }}
\def\stylm{\displaystyle }
$
Analiza Matematyczna 2.
O zadaniu 762. z Listy 15.
ZADANIE 762.
Wyznaczyć wszystkie funkcje $f : \RR\to \RR$, dla których $ f'(x)=|\sin x|.$
Uwaga 0.
Poniżej, kolorem zielonym są pisane moje (= K.O.) wtrącenia, które
nie powinny znaleźć się w formalnym rozwiązaniu.
Uwaga 1.
W zadaniu występuje |.| - wartość bezwględna - co kojarzy się z ostrzem wykresu funkcji $y=|x|$, czyli z brakiem pochodnej w punkcie $x=0$.
JEDNAK tu nie mamy obliczać pochodną, ale 'wręcz przeciwnie', mamy całkować, mamy znaleźć funkcję $f$, której pochodną $f'$ widzimy.
ZATEM owe skojarzenie JEST BEZ ZWIĄZKU z zadaniem.
Jak się za to zabrać? Najpierw 'pozbędziemy się' wartości bezwględnej (a jednak!?).
Zauważmy, że
$$
\begin{array}{ccl}
\sin x = 0 & \mbox{dla} & x=k\pi,\ \ k\ \mbox{ całkowite }\\
\sin x > 0 & \mbox{dla} & x\in(k\pi,k\pi+\pi),\ \ k\ \mbox{ całkowite parzyste}\\
\sin x < 0 & \mbox{dla} & x\in(k\pi,k\pi+\pi),\ \ k\ \mbox{ całkowite nieparzyste}
\end{array}$$
Zatem
$$f'(x)=|\sin x|=\left\{
\begin{array}{ccl}
0 & \mbox{dla} & x=k\pi,\ \ k\in\ZZ\\
\sin x & \mbox{dla} & x\in(k\pi,k\pi+\pi),\ k\in\ZZ,\ k \mbox{ parzyste}\\
-\sin x & \mbox{dla} & x\in(k\pi,k\pi+\pi), \ k\in\ZZ, \ k \mbox{ nieparzyste}
\end{array}\right. .$$
Oj! Te 'klamerki"! Jak tu się ich pozbyć?
Inaczej pisząc:
$$f'(x)=\left\{
\begin{array}{ccl}
0 & \mbox{dla} & x=k\pi,\ \ k\in\ZZ\\
(-1)^k\sin x & \mbox{dla} & x\in(k\pi,k\pi+\pi),\ k\in\ZZ
\end{array}\right. .$$
Oj$^2$! Dalej są 'klamerki"!
Ponieważ na końcach tych przedziałów z obu wzorów TEŻ mamy 0, więc
$f'(x)=(-1)^k\sin x,\ \ \mbox{dla}\ \ x\in[k\pi,k\pi+\pi)$
(dla prostoty zapisów poniżej przyjmujemy stale, że $k$ jest liczbą całkowitą).
Można też tak: $\ \ f'(x)=(-1)^k\sin x,\ \ \mbox{dla}\ \ x\in(k\pi,k\pi+\pi],\ k\in\ZZ.\ $
A czy można 'siak': $\ \ f'(x)=(-1)^k\sin x,\ \ \mbox{dla}\ \ x\in[k\pi,k\pi+\pi],\ k\in\ZZ\ $ ?
Niby tak, ale 'ostrożnie z tym napisem'! (Dlaczego?) Zatem pozostańmy przy wersji [...).
Dotychczasowe rozważania o pozbywaniu się 'klamerek' można zapewne pominąć w formalnym opisie rozwiązania.
Nie wiem, czy bym odjął choć 1 punkt, gdyby zapis rozwiązania zaczynał się dopiero teraz, następująco:
Na początek zauważmy, że $\ \ f'(x)=(-1)^k\sin x,\ \ \mbox{dla}\ \ x\in[k\pi,k\pi+\pi)\ $
(patrz rys.).
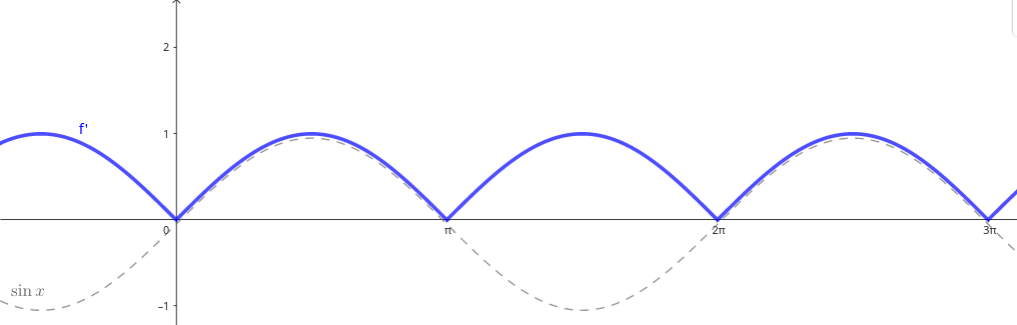
bowiem 'prawdziwa zabawa' jeszcze się nie zaczęła. Zatem zacznijmy wreszcie!
Oczywiste jest (tw. z wykładu), że na każdym z PRZEDZIAŁÓW OTWARTYCH $(k\pi,k\pi+\pi)$ z osobna,
szukana funkcja $f$ jest równa albo $\ -\cos x+const,\ $ albo $\ \cos x+const\ $
(w zależności od parzystości $k$).
CAŁA trudność zadania polega na tym: JAKIE są owe stałe? (Np.: Czy muszą być jednakowe? Czy mogę być jednakowe?...)
Rozważmy zatem taką funkcję $\ g:\RR\to\RR\ $ (zależną od nieskończenie wielu parametrów $C_k$), dla której
$g(x)=(-1)^{k+1}\cos x + C_k,\ \ \mbox{dla}\ \ x\in(k\pi,k\pi+\pi).$
Przy odpowiednich stałych $C_k$, szukana funkcja $f$ jest zgodna z $g$ na tych przedziałach OTWARTYCH; $\ g'(x)=f'(x).$
Dalej wystarczy zbadać punkty postaci $k\pi$.
Zobaczmy 'co się dzieje w okolicach' $x=\pi$ i $x=2\pi$ :
Co widać w $x=\pi$ ?
Mamy:
$\ \ \lim\limits_{x\to \pi^-}g(x)=\lim\limits_{x\to \pi^-}-\cos x+C_{0}=-\cos\pi+C_0=C_0+1, \ \ $
oraz
$\ \ \lim\limits_{x\to \pi^+}g(x)=\lim\limits_{x\to \pi^+}\cos x+C_{1}=\cos\pi+C_1=C_1-1.$
Zatem, aby $g$ była różniczkowalna w $\pi$, to musi być ciągła, więc musi być spełniony warunek
$\ g(\pi)=C_0+1=C_1-1,\ $ czyli $\ C_1=C_0+2. $
Identyczny rachunek pokazuje ogólnie: $\ C_{2j+1}=C_{2j}+2. $
Co widać w $x=2\pi$ ? Niemal to samo:
Mamy:
$\ \ \lim\limits_{x\to 2\pi^-}g(x)=\lim\limits_{x\to 2\pi^-}\cos x+C_{1}=\cos2\pi+C_1=C_1+1, \ \ $
oraz
$\ \ \lim\limits_{x\to 2\pi^+}g(x)=\lim\limits_{x\to 2\pi^+}-\cos x+C_{2}=-\cos2\pi+C_2=C_2-1.$
Zatem, aby $g$ była różniczkowalna w $2\pi$, to musi być ciągła, więc musi być spełniony warunek
$\ g(2\pi)=C_1+1=C_2-1,\ $ czyli $\ C_2=C_1+2. $
Identyczny rachunek pokazuje ogólnie: $\ C_{2j}=C_{2j-1}+2. $
Czy to wszystko trzeba pisać w rozwiązaniu? Nie! Ogólnie jest łatwiej!?
Aby $g$ miała pochodne w punktach $k\pi$ musi być w tych punktach ciągła, w szczególności muszą istnieć i być równe granice jednostronne w $k\pi$:
$\stylm\ \ \lim\limits_{x\to k\pi^+}g(x)=\lim\limits_{x\to k\pi^-}g(x).$
Obliczmy je ( uwzględniając, że $\cos k\pi=(-1)^k\ $ ) :
$\stylm \ \ \bullet \ \ \ \ \lim\limits_{x\to k\pi^+}g(x)= \lim\limits_{x\to k\pi^+}(-1)^{k+1}\cos x+C_k=(-1)^{k+1}\cos k\pi+C_k= C_k-1,$
$\stylm \ \ \bullet \ \ \ \ \lim\limits_{x\to k\pi^-}g(x)=\lim\limits_{x\to k\pi^-}(-1)^{(k-1)+1}\cos x+C_{k-1}=(-1)^{k}\cos k\pi+C_{k-1}= C_{k-1}+1.$
Stąd ich równość daje zależność $\stylm\ \ C_{k}=C_{k-1}+2\ \ $ (postęp arytmetyczny). Zatem $\ \ C_k=C_0+2k.$
Gdy ponadto $\ g(k\pi)$ jest równe owym granicom czyli $\ g(k\pi)=C_k-1=C_0+2k-1,\ $ to $g$ jest ciągła (w każdym punkcie).
Otrzymujemy (przyjmując $\ C=C_0$):
$$g \mbox{ jest ciągła wtedy i tylko wtedy, gdy dla pewnego $C$ jest postaci }
\ \ g(x)=(-1)^{k+1}\cos x + C+2k,\ \ \mbox{dla}\ \ x\in[k\pi,k\pi+\pi).$$
Niestety to jeszcze nie koniec, TRZEBA SPRAWDZIĆ, że dla ciągłej $g$ jak wyżej ISTNIEJE $\ g'(k\pi)$, i że jest równe $0=|\sin k\pi|.$
Czy trzeba obliczać wprost z definicji? Niekoniecznie.
Na koniec sprawdzimy, że ciągłość $g$ wystarcza do uzasadnienia, że istnieją $g'(k\pi)$ i są równe $0=|\sin k\pi|=f'(k\pi).$
Z ciągłości wynika, że dla $n\in\ZZ$ mamy $\stylm\ g|_{[n\pi,n\pi+\pi]}(x)=(-1)^{n+1}\cos x+C+2n,\ $
czyli mamy jeden wzór, który obowiązuje również na końcach tego przedziału.
Zatem na końcach można obliczać pochodne jednostronne prosto ze wzorów.
W obu końcach dostajemy TĄ samą wielkość $\pm0=0$, więc $g'(k\pi)=0. $
Odpowiedź.
$$f'(x)=|\sin x| \mbox{ dla każdego $x$ wtedy i tylko wtedy, gdy dla pewnego $C$ jest postaci }
\ \ f(x)=(-1)^{k+1}\cos x + C+2k,\ \ \mbox{dla}\ \ x\in[k\pi,k\pi+\pi).$$
Oj trudne! Trudne nie są rachunki, tylko co?
Rozumowania, które pozwalają 'obejść' rachunki.
A po co była ta funkcja $g$? Mnie potrzebna była do wysławiania rozumowania; BEZ niej też można, ale wydawało mi się, że tak będzie klarownie.
Uwaga 2.
Można się zastanawiać, czy $f$ można zapisać JEDNYM wzorem, BEZ owego całkowitego $k$.
Można, na przykład $\stylm \ \ f(x)=(-1)^{[x{/}\pi]+1}\cos x+C+2\cdot [x{/}\pi].\ $
Owa część całkowita $[x{/}\pi]$ wyznacza $k$. Jest to tylko - w pewnym sensie - zaszyfrowanie poprzedniego wzoru.
Uwaga 3.
Wykres funkcji $f$ jest podobny (w potocznym sensie słowa 'podobny') do wykresu funkcji $\ y=x+\sin x.\ $
Ciekawy jest poniższy problem:
ZADANIE 762'.
Czy dla każdej funkcji $f$ z zadania 762 istnieją takie stałe $p,q,r,s,t$, że $\stylm\ \ f(x)=p\cdot x+q\cdot \cos(r\cdot x+s)+t,\ $ dla każdego $\ x\in\RR$?
Uwaga 4.
W zadaniu 762. dana funkcja $f'$ jest okresowa. Czy to jest istotne dla pomysłu rozwiązania?
Zamiast 'spekulować' proszę spróbować powalczyć z poniższym:
ZADANIE 762''.
Wyznaczyć wszystkie funkcje $f : (0,+\infty)\to \RR$, dla których $ f'(x)=|x\sin x^2|.$
Ciekaw jestem Państwa rozwiązań.
Mam nadzieję, że powyższa moja pisanina okaże się dla kogoś przydatna.
Mam też nadzieję2, że w powyższym tekście jest nie za dużo bledow (i pomylek).
(Za wskazanie takowych będę wdzięczny.)
Krzysztof Omiljanowski
