Dopasować okrąg

POSTAWIENIE PROBLEMU

Wyznaczyć 'najlepiej dopasowany' okrąg w punkcie W = [x(t0), y(t0)] do krzywej zadanej parametrycznie: x = x(t), y = y(t).

Np. środkowy okrąg wygląda na 'najlepiej dopasowany' spośród trzech na rysunku dla paraboli w jej wierzchołku W

> "Jak sprecyzować pojęcie 'najlepiej dopasowany okrąg'? Jak go znaleźć?":

Pomocnicze procedury

>

>

>

Uwaga: w MAPLE'u są takie funkcje jak: odległość, iloczyn skalarny; jednak poniżej definiujemy WŁASNE (dla wygody?).

>

PRZYKŁAD

dla paraboli y=x^2 w wierzchołku W (dla młodszego licealisty)

> W "pobliżu" wierzch. W paraboli wybieramy symetrycznie punkty A,B

> Dla trójkąta WAB środek S okręgu opisanego leży oczywiście na osi OY .

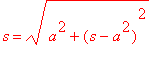> Warunek SW = SA (zapisany analitycznie) pozwoli wyznaczyć współrzędną s środka S.

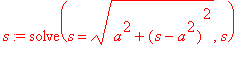> Rozwiązujemy więc to równanie (na papierze równie łatwo):

Zatem widać, że gdy A,B są blisko W , czyli gdy a jest "malutkie", to wartość s jest prawie równa 1/2.
Stąd "najlepiej dopasowany" okrąg ma środek w S = [0, 1/2 ] i promień 1/2 (uruchom poniższą animację).

> r:=s:display({plot(x^2,x=-1.3..1.3,color=blue),animate({okr,seq([t*a*j,t*a^2,t=0..1],j=[-1,1]),[a*(1-2*t),a^2,t=0..1]},a=-1..0,color=red)});

>

POMYSŁ I..

Środki P =[ xp, yp ] okręgów opisanych na trójkątach ABC dla punktów A,B,C tej krzywej, bliskich punktowi W, "powinny" przybliżać środek S1 szukanego okręgu.

Uwaga: w MAPLE'u są takie funkcje jak: odległość, iloczyn skalarny; jednak poniżej definiujemy WŁASNE (dla wygody?).

>

> ("techniczne wyczyszczenie" zmiennych)

>

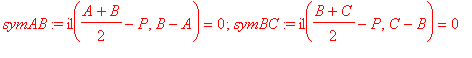> symetralne odcinków AB i BC

> przecięcie symetralnych

> przypisanie zmiennym xp, yp obliczanych wartości (już MAPLE 'tak ma')

>
szukane S1 jest granicą P=[xp,yp]

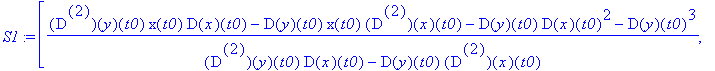
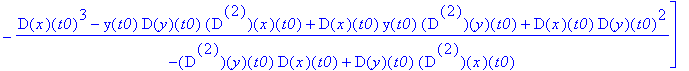
TO Trochę straszne; D to operator pochodnej -- częste w MAPLE'u .

> r1 :=simplify(odl(W,S1)); promień 'najlepiej dopasowanego okręgu' jest oczywiście równy odległości punktów W i S

>

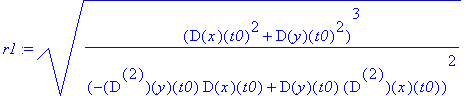
Zastosowanie.

Definiujemy krzywą (parametrycznie):

> x:=t->t;
y:=t->cos(t)-3/4;

> teraz środek S i promień r wyznaczonego okręgu zależą (tylko) od t0

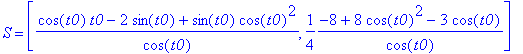
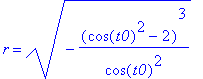
Np. dla t0 = mamy:

>

Na koniec trochę obrazków (szczegóły MAPLE'a są trochę 'okrutne' -- może można je pominąć?):

>

Proszę oglądnąć w przypadku innych krzywych (wystarczy zmienić definicję x(t) i y(t) )

POMYSŁ II.

Punkty Q =[ xq, yq ] przecięcia normalnych (tj. prostopadłych do krzywej) wystawionych w punktach A,W tej krzywej, gdy A jest bliskich punktowi W , "powinny" przybliżać środek S2 szukanego okręgu.

> (to "techniczne wyczyszczenie" zmiennych)

>

> wektory styczne do krzywej w A i W

> normalne w A i B

> przecięcie normalnych

> przypisanie zmiennym xq, yq obliczanych wartości (już MAPLE 'tak ma')

> szukane S2 jest granicą Q

> r2:='odl(W,S2)'; promień 'najlepiej dopasowanego okręgu' jest równy odległości punktów W i S

>

Zastosowanie.

Definiujemy krzywą parametrycznie:

> x:=t->t;
y:=t->t^2/3-3;

> teraz środek S i promień r wyznaczonego okręgu zależą (tylko) od t0

Np. dla t0 = 1 mamy:

>

Na koniec trochę obrazków (szczegóły MAPLE'a są trochę 'okrutne' -- może można je pominąć?):

>

Proszę oglądnąć w przypadku innych krzywych (wystarczy zmienić definicję x(t) i y(t) )

POMYSŁ III.

Dla punktu M tej krzywej (bliskiegu punktowi W ), znajdujemy okrąg przechodzący przez W i M o środku N =[ xn, yn ] na normalnej (prostopadłej) do krzywej wystawionej w punkcie W. Punkt N "powinien" przybliżać środek S3 szukanego okręgu.

> ("techniczne wyczyszczenie" używanych zmiennych)

>

> wektor styczny do krzywej w punkcie W

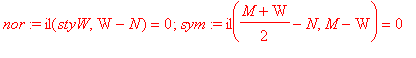> normalna w W oraz symetralna odcinka MW

> ich przecięcie

> przypisanie zmiennym xn, yn obliczanych wartości (już MAPLE 'tak ma')

> szukane S3 jest granicą N

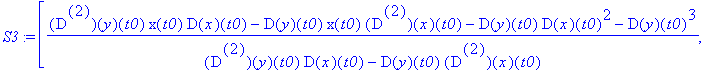
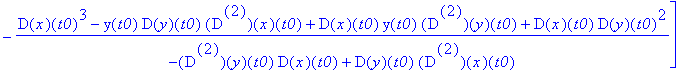
> promień 'najlepiej dopasowanego okręgu' jest oczywiście równy odległości punktów W i S

>

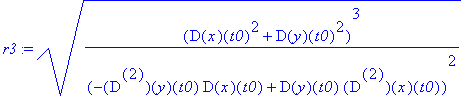
Zastosowanie.

Definiujemy krzywą parametrycznie:

> x:=t->t;
y:=t->t*(t-1)*(t+2)/3+1;

> teraz środek S i promień r okręgu zależą (tylko) od t0

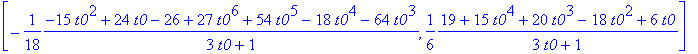
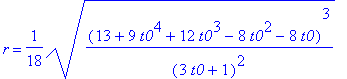
Np. dla t0 = -1 mamy:

>

Na koniec trochę obrazków (szczegóły MAPLE'a są trochę 'okrutne')::

>

Proszę oglądnąć w przypadku innych krzywych (wystarczy zmienić definicję x(t) i y(t) )

PODSUMOWANIE

Czy te pomysły dają TEN SAM efekt? Czy S1 = S2 = S3 ???

Dla konkretnej krzywej:

> x:=t->t;
y:=t->t^3-t^2+3/4;

> 'S1'=S1;'r1'=r1;
'S2'=S2;'r2'=r2;
'S3'=S3;'r3'=r3;

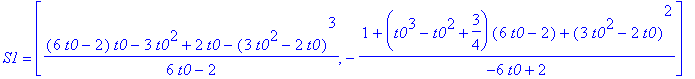
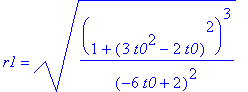
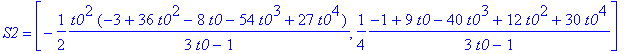
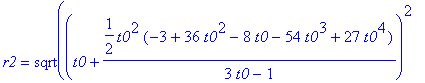
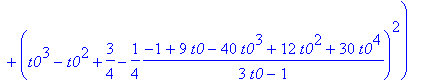
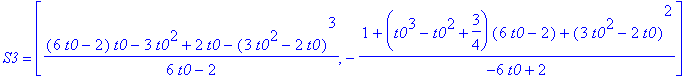
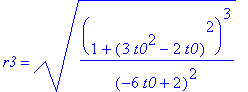
Można 'zmusić' MAPLE'a by sprawdził za nas czy S1 = S2 = S3 oraz r1 = r2 = r3 :

> 'S1 - S2'= simplify( S1 - S2);
'S2 - S3'= evala( S2 - S3);
'r1 - r2'= simplify( r1 - r2);
'r2 - r3'= simplify( r2 - r3);

Dla innej krzywej mamy:

> x:=t->t;
y:=t->t^4-2;

> 'S1'=simplify(S1),'r1'=simplify(r1);
'S2'=simplify(S2),'r2'=simplify(r2);
'S3'=simplify(S3),'r3'=simplify(r3);

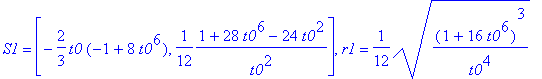
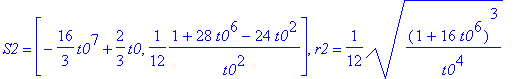
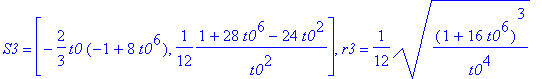
Można 'zmusić' MAPLE'a by sprawdził za nas czy S1 = S2 = S3 oraz r1 = r2 = r3 :

> 'S1 - S2'= simplify( S1 - S2);
'S2 - S3'= simplify( S2 - S3);
'r1 - r2'= simplify( r1 - r2);
'r2 - r3'= simplify( r2 - r3);

A ogólnie? (Najpierw 'wykasujemy' definicje krzywej)

> x:='x'; y:='y';

> 'S1'=simplify(S1),'r1'=simplify(r1);
'S3'=simplify(S3),'r3'=simplify(r3);

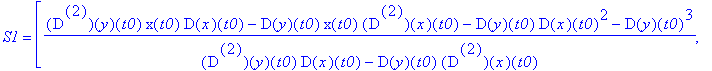
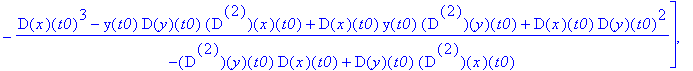
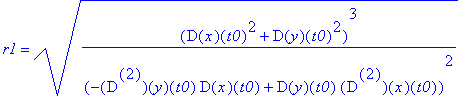
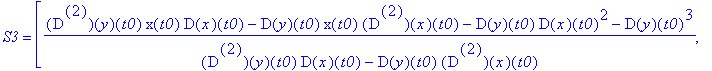
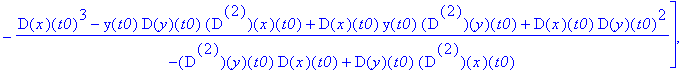
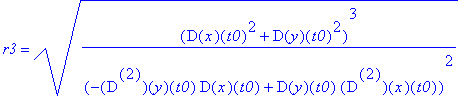
Słabo widać, więc "zmuśmy" MAPLE'a by uprościł różnice:

> 'r1 - r3' = simplify(r1-r3);
'S1 - S3' = simplify(S1-S3);

Zera są dowodem tożsamości: S1 = S3 i r1 = r3 !!! TO JEST DOWÓD !!!

(Pomijamy tu dowód S1 = S2 i r1 = r2 .) Oczywiście otrzymane wzory ogólne są poprawne przy pewnych założeniach, czego tu nie będziemy analizować.

Uwaga: w podręcznikach analizy matematycznej znaleziony tu "najlepiej dopasowany" okrąg nazywa się okręgiem krzywizny , jego środek -- środkiem krzywizny , promień -- promieniem krzywizny , a odwrotność promienia -- krzywizną krzywej w punkcie W.