>
![]()
>
![]()
![[Maple Plot]](a1b1/a=1_b=13.gif)
Gdy po
zielonym, nieruchomym okręgu o promieniu
a
=1
toczy się
okrąg niebieski o promieniu
b
=1
, to
ustalony punkt
niebieskiego okręgu 'biegnie' po
krzywej zwanej kardioidą
. Oto
jej
opis (kard):
>
![]()
>
![]()
>
![]()
>
![]()
![]()
Poniżej typowy zapis parametryczny kardioidy kard:
>
![]()
![]()
![]()
![]()
Wygląda jak niżej (warto pominąć szczególy tych formul):
>
w:=k->plot([[op(okra),t=0..zakr],[((a+b)*cos(zakr*k/m),(a+b)*sin(zakr*k/m))+op(okrb),t=0..zakr],[op(kard),t=0..zakr*k/m],
[op(kard-[c1*b*cos(T),c1*b*sin(T)]),t=0..zakr*k/m],[op(kard+[c1*b*cos(T),c1*b*sin(T)]),t=0..zakr*k/m]],
color=[green,blue,red,brown,cyan]):display([seq(w(k),k=1..m)],insequence=true, scaling=CONSTRAINED);
![[Maple Plot]](a1b1/a=1_b=113.gif)
Wektor prędkości czerwonego punktu i jego dlugość dl :
>
![]()
![]()
>
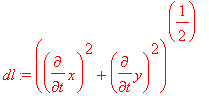
![]()
Dlugosc kardioidy:
>
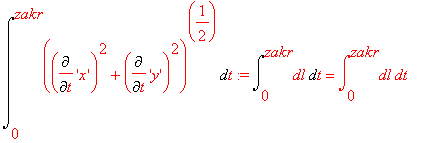
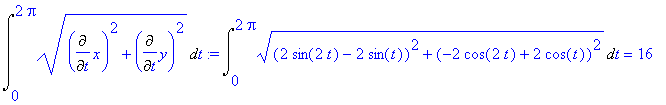
> evalf(int( dl, t=0..zakr));
![]()
Pole ograniczone kardioidą (z malym blędem - jakim?):
>
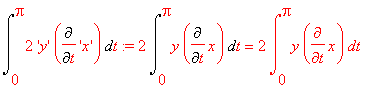
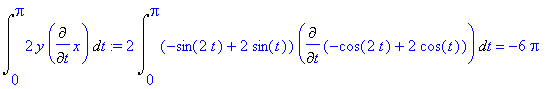
Gdy na promieniu niebieskiego okręgu zaznaczymy brązowy punkt i na przedlużeniu (tego promienia) punkt blękitny , to wykreślą trochę inne krzywe ( warto pominąć szczególy tych formul ):
> c1:=1/2:w1:=k->plot([[op(okra),t=0..zakr],[((a+b)*cos(zakr*min(1, k/m)) ,(a+b)*sin(zakr*min(1,k/m)))+op(okrb),t=0..zakr], [op(kard),t=0..zakr*k/m],[op(kard-[c1*b*cos(T),c1*b*sin(T)]),t=0..zakr*k/m],[op(kard+[c1*b*cos(T),c1*b*sin(T)]),t=0..zakr*k/m]],color=[green,blue,red,brown,cyan]):display([seq(w1(k),k=1..2*m)],insequence=true, scaling=CONSTRAINED);
![[Maple Plot]](a1b1/a=1_b=123.gif)
Opis tych krzywych: przyjmujemy stalą c oznaczającą który punkt promienia będzie kreślil krzywą i nieznacznie modyfikujemy stare wzory (wlaściwie tylko kard; resztę kopiujemy BEZ ZMIAN):
>
![]()
![]()
>
![]()
![]()
![]()
![]()
>
![]()
![]()
>
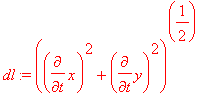
![]()
Przyjmujemy do obliczeń c=1/2. Dlugosc takiej NOWEJ kardioidy:
>
![]()
>
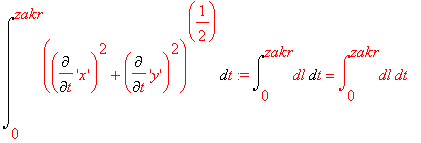
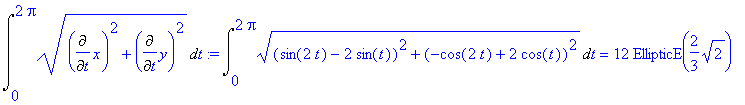
Co upraszcza się do:
> evalf(int( dl, t=0..zakr));
![]()
Jej pole (też z blędem):
>
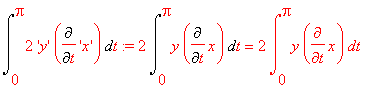
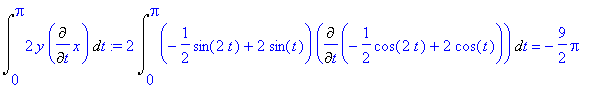
Przyjmujemy do obliczeń c=3/2. Dlugosc takiej NOWEJ kardioidy:
>
![]()
>
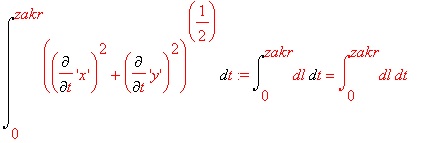
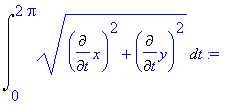
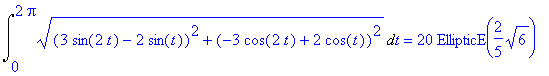
Co upraszcza się do:
> evalf(int( dl, t=0..zakr));
![]()
Jej pole (też z blędem):
>
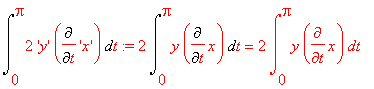
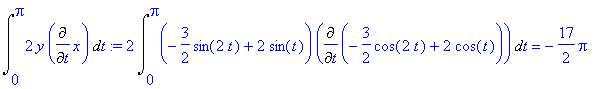
>