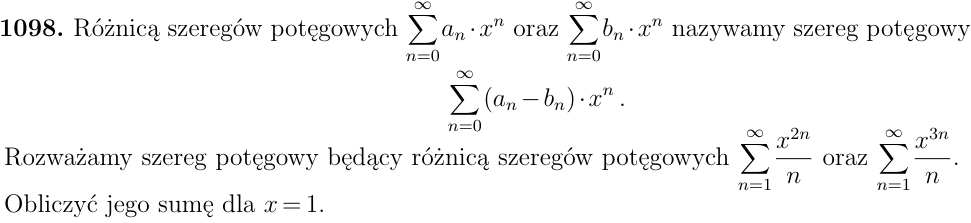
K.O. Konsultacje: AM2, zad. 1098, Lista 23 . (różnica szeregów potęgowych)
Omówię zadanie 1098 z Listy 23 >>> autorstwa Jarosława Wróblewskiego.
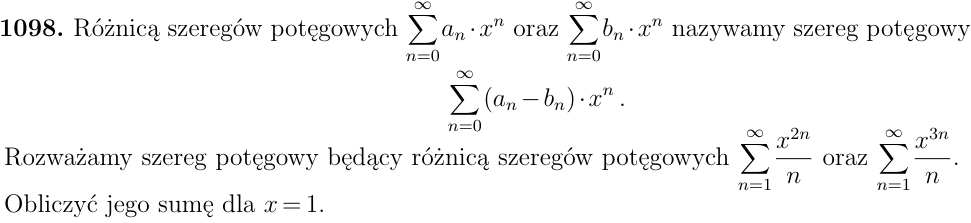
Celem zadania jest obliczenie sumy szeregu $\ \sum\limits_{m=1}^\infty \stylm c_m\!\cdot\!x^{m}\ $ dla $x=1$,
czyli sumy szeregu (liczbowego):
$ \sum\limits_{m=1}^\infty c_m =
0\!\cdot\! 1^{1}+ (\frac{1}{1}\!-\!0)\!\cdot\! 1^{2}+
(0\!-\!\frac{1}{1})\!\cdot\! 1^{3}+
(\frac{1}{2}\!-\!0)\!\cdot\!1^{4}+
0\!\cdot\! 1^{5}+
(\frac{1}{3}\!-\!\frac{1}{2})\!\cdot\!1^{6}+
0\!\cdot\! x^{7}+
(\frac{1}{4}\!-\!0)\!\cdot\!1^{8}+
(0\!-\!\frac{1}{3})\!\cdot\!1^{9}+
(\frac{1}{5}\!-\!0)\!\cdot\!1^{10}+
\ldots
$
Kluczowa obserwacja: ( jak nie widać, to może zapisz 'z kropeczkami...' )
(2.1) $\stylm S_{6k}=\sum\limits_{i=1}^{6k}c_i=
\sum\limits_{i=1}^{3k}\frac{1}{i}\ - \sum\limits_{i=1}^{2k}\frac{1}{i}
= \sum\limits_{i=2k+1}^{3k}\frac{1}{i}= $
$\stylm \frac{1}{2k+1}+\frac{1}{2k+2}+\frac{1}{2k+3}+\ldots+\frac{1}{3k}\ \ $
Druga kluczowa obserwacja: można w ostatnim napisie dostrzec sumę Riemanna:
( całki z funkcji $\frac{1}{x}$ )
(2.2) $\stylm S_{6k} = \sum\limits_{i=2k+1}^{3k}\frac{1}{i}=
\sum\limits_{i=2k+1}^{3k} \frac{1}{i \over k}\cdot \frac{1}{k}\ \ \ \mathop{\longrightarrow}_{k\to\infty} \ $
$\stylm \ \int_2^3\frac{1}{x}\:dx=$ $\stylm\ln \frac{3}{2}.\ \ $
Uwaga.
To 'prawie koniec' rozwiązania; trzeba tylko uzasadnić, że
cały ciąg $(S_m)$ ma tą samą granicę, co jego podciąg $(S_{6k})$.
Przydatne będzie oszacowanie:
(2.3) $\stylm |S_{6k+j}-S_{6k}| < \frac{1}{3k}\ $ dla $\ j\in\{0,1,2,3,4,5\}\ $ i $k\in\NN.$
Aby uzasadnić (2,3) wystarczy przyglądnąć się wyrazom $c_m$:
$\stylm c_{6k}=\frac{1}{3k}-\frac{1}{2k},\ c_{6k+1}=0,\ c_{6k+2}=\frac{1}{3k+1},\ c_{6k+3}=-\frac{1}{2k+1},\ c_{6k+4}=\frac{1}{3k+2},\ c_{6k+5}=0$
i sprawdzić, że największa z różnic w (2.3) jest równa $\stylm |S_{6k+2}-S_{6k}|=\frac{1}{3k+1}\ $.