$ \def\RR{\mathbb{R}} \def\NN{\mathbb{N}} \def\CC{\mathbb{C}} \def\QQ{\mathbb{Q}} \def\dint{\mathop{\int\!\!\int}} \def\tint{\mathop{\int\!\!\int\!\!\int}} \def\rot{\hbox{rot\hskip2truept }} \def\div{\hbox{div\hskip2truept }} \def\grad{\hbox{grad\hskip2truept }} \def\zad#1{\noindent {\bf #1. }} \def\zadp#1{\mbox{\hspace{1em} {\bf #1) }}} \def\zadpa{\zadp{a} } \def\zadpb{\zadp{b} } \def\zadpc{\zadp{c} } \def\zadpd{\zadp{d} } \def\stylm{\displaystyle } $

Konsultacje: Groch z kapustą 1 (przed egz. lic.). 

ZADANIE 1.

ROZWIĄZANIE 1 ('tajemnicze').
Niech $S_{37}$ oznacza grupę wszystkich permutacji zbiotu $\{1,2,\ldots,37\}$ (mnożenie rozumiemy jako składanie, notowane 'od prawej').
Rozważmy następujęce iloczyny cykli (transpozycji):
    $a=(1,3) (4,37)(5,36)(6,35)\ldots(19,22)(20,21)$,
    $b=(1,2) (3,37)(4,36)(5,35)\ldots(18,22)(19,21)$.
Ponieważ są to iloczyny cykli o rozłącznych dziedzinach, więc ich rzędy są równe 2.
Na koniec zauważmy, że $\ ab=(1,2,3,4,5,\ldots,36,37),\ $ czyli jest jest cyklem długości 37, więc ma rząd równy 37.

Uwaga. Podgrupa generowana przez elementy $a,b$ jest izomorficzna z grupą symetrii własnych 37-kąta foremnego.
 

 
ROZWIĄZANIE 2 ('odtajnione').
Rozważmy izomotrie $\RR^2$: niech $s_k$ oznacza odbicie względem prostej $\ \ y=\tan\left(k\cdot \frac{2\pi}{2\cdot 37}\right)\cdot x,\ \ $, dla $k\in\{0,1,\ldots ,36\}$.
Niech $G$ oznacza podgrupę wszystkich izometrii $\RR^2$ generowaną przez $\{s_0,s_1,\ldots,s_{36}\}$ (ze złożeniem jako działaniem).
Oznaczmy: $a=s_0$ oraz $b=s_1$.
    Oczywiście $\ a a ={\rm id}\ $ oraz $\ b b ={\rm id}, \ $ więc $a,b$ mają rzędy równe 2.
    Ponieważ złożenie $\ a b \ $ jest obrotem wzgledem $(0,0)$ o dwukrotność kąta pomiędzy ich osiami, więc jest obrotem o kąt $\frac{2\pi}{37}$.
Zatem rząd $ab$ jest równy 37.
 
 

ZADANIE 2.

Wskazówka.

  $\bullet$   Znajdź długości ? oraz ??
  $\bullet$   GDZIE tu jest 24?
  $\bullet$   Jest tak, czy siak? (JAK to sprawdzić rachunkiem?)
  $\bullet$   GDZIE tu jest $\ \int\limits_1^5\sqrt{x^2+24}\;dx\ $ (zamaluj)?
 
 
 

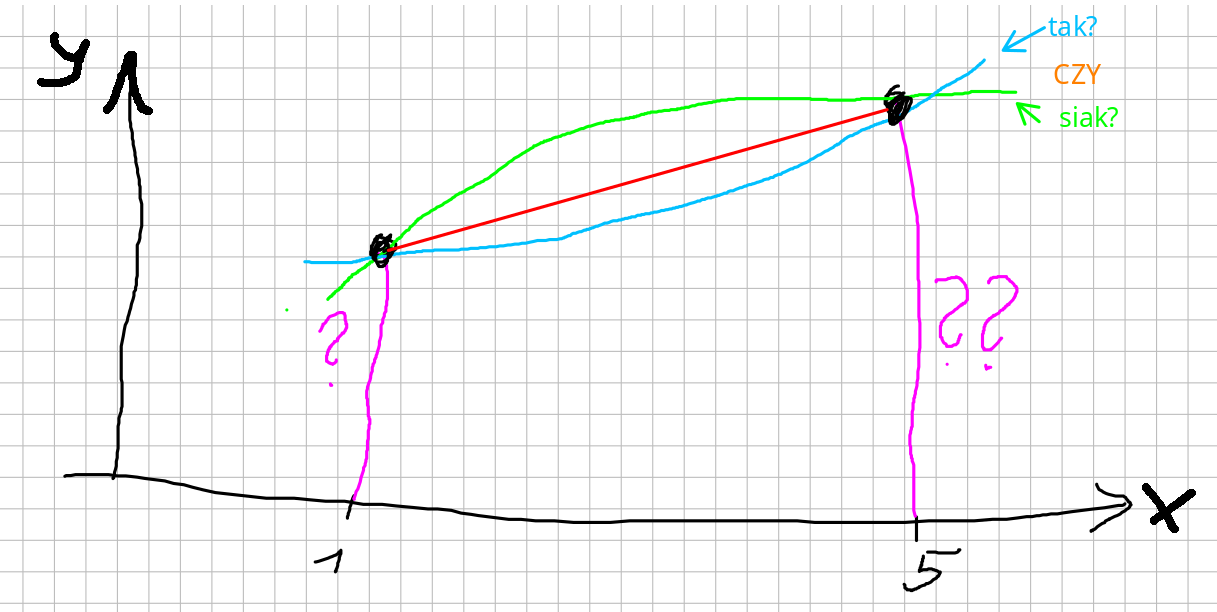
ZADANIE 3.

Wskazówka.
NIE, pomyśl o obrocie względem (0,0) o kąt $\ \frac{2\pi}{7}\ $ i
zapisz macierz obrotu $A=\left(\matrix{ \cos\frac{2\pi}{7}& ??? \\ ??? & ??? }\right)$
 
 

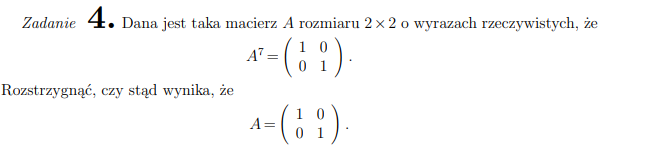
ZADANIE 4.

Wskazówka.
TAK, pomyśl o obrocie względem (0,0) o kąt $\frac{2\pi}{4}$ (czyli 90o) i
zapisz macierz obrotu $B=\left(\matrix{ 0 & 1 \\ ??? & 0 }\right)$.
To jeszcze nie koniec:
Oblicz $B^2=\left(\matrix{ ... & ... \\ 0 & ... }\right)$.
Na koniec 'wymość' $A$ z macierzami $B$.
i sprawdź (rachunkiem?), że $A^2=-{\rm 1\!I}$.
 
 

ZADANIE 43.
Rozstrzygnąć, czy istnieje taka macierz $A$ rozmiaru (3 × 3) o wyrazach rzeczywistych, że $A^2=\left(\matrix{ -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1}\right)$.

Wskazówka.
Nie, pomyśl o wyznaczniku.
Dokładniej:
Gdyby istniała taka macierz $A$, to wtedy jej wyznacznik musiałby spełniać pewne równanie. (JAKIE?)
Ale to równanie nie ma rozwiązań (rzeczywistych).