Programowanie współbieżne - poblemy

Problem 1

Operator (macierz) A przekształca funkcje dwu zmiennych dyskretnych w siebie i jest zadany wzorem

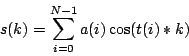
(Af)(i,k) = f(i+1,j) + f(i-1, j) + f(i, j+1) + f(i, j-1)

gdzie i,j przebiega zakres 0..N. We wzorze powyżej przyjmujemy że f(i,j) jest równe 0 jesli i lub j jest poza zakresem. Prostą metodą szukania wartości i wektorów własnych macierzy jest metoda potęgowa: wielokrotnie przykładamy macierz A do tego samego wektora otrzymując wektory A^nf. Zwykle już dla niezbyt dużych n A^nf jest bliskie wektora własnego. Wtedy odpowiednią wartość własną można obliczyć jako iloczyn skalarny A^(n+1)f i A^nf. Metodę tę można zrównoleglić dzieląc kwadrat [0..N]x[0..N] na mniejsze kwadraty i obliczając niezależnie wartości Af w każdym z mniejszych kwadratów. Ponieważ do obliczenia wartości Af na kwadracie potrzebujemy wartości f na kwadracie o boku o 1 większym w każdym kroku obliczeń trzeba rozsyłac obliczone wartości Af przy brzegach kwadratów naszego podziału, tak by były dostępne w następnym kroku.

Problem 2

Dane są tablice a i t (obie wielkości N). Obliczyć

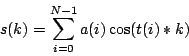
$\begin{displaymath} s(k) = \sum_{i=0}^{N-1} a(i)\cos(t(i)*k)\end{displaymath}$

dla k=0,...,M i następnie znaleźć 10 największych wartości s(k). Obliczenia zorganizować tak by każdy wątek znał tablice a i t (zakładamy że są one niezbyt duże) i obliczał s(k) dla k z pewnego przedziału (zakładamy że M jest duże i że warto podzielić przedział [0, M] na podprzedziały). Wątek głowny ma rozdzielać kolejne przedziały do obliczenia pomiędzy wątki robocze.

Komentarz1: Jest to uproszczona wersja zagadnienia analizy okresowości, w praktycznych zastosowaniach trzeba również policzyć podobną sumę w której występuje sinus.

Komentarz2: Aby uzyskać rozsądną szybkość trzeba uniknąć ciągłego obliczania kosinusów. Dlatego lepiej obliczać kosinusy i sinusy przy pomocy funkcji bibliotecznej dla początkowego k, zaś dla k+1 obliczać kosinusy (i sinusy) używając wzory na kosinus sumy kątów.

Problem 3

Oblicznie najwiekszego wpólnego dzielnika wielomianów wielu zmiennych. Największy wspólny dzielnik wielomianów jednej zmiennej nad ciałem można obliczać przy pomocy znanego algorytmu Euklidesa. Dla wielomianów niezbyt dużego stopnia jest to metoda bliska optymalnej. W przypadku wielomianów wielu zmiennych trzeba stosować bardziej skomplikowane metody. Jedna możliwa technika bazuje na chińskim twierdzeniu o resztach, a właściwie na interpolacji Lagranga. Mianowicie niech P i Q będą wielomainami dwu zmiennych. Oznaczmy przez P_y wielomian zadany wzorem

P_y(x) = P(x, y)

tzn. P_y powstaje przez podstawienie y za drugą zmienną w P. Podobnie określamy Q_y. Nie jest prawdą że zawsze

NWD(P, Q)_y = NWD(P_y, Q_y)

jednakże równość powyżej zachodzi dla wielu y (jest tylko skończenie wiele wartości dla których t równość nie zachodzi).

Oznacza to że można stosować następującą metodę obliczania wspólnego dzielnika: obliczany NWD(P_y, Q_y) dla pewnej ilości wartości y (zależnie od stopnia wielomianu P i Q), następnie odtwarzamy NWD(P, Q) z NWD(P_y, Q_y) używając interpolacji Lagrange'a. Dokładniej, traktujemy NWD(P, Q) jako wielomian względem x którego współczynniki są wielomianami względem y. Dla każdego współczynnika z osobna możemy teraz stosować interpolację Lagrange'a.

Uwaga1: W tym zadaniu obliczenia należy prowadzić modulo wybraną liczbę pierwszą p, w ten sposób nasze współczynniki są ciałem.

Uwaga2: ogólnie NWD jest określony z dokładnością do stałej, co przeszkadza przy interpolacji. Jednakże, jeśli jeden z wielomianów P lub Q ma 1 jako wspólczynnik przy największej potędze x to można NWD(P_y, Q_y) unormować tak by miał 1 jako wspólczynnik przy największej potędze x. W ogólnym przypadku trzeba stosować nieco bardziej skomplikowaną metodę.

Uwaga3: Naszkicowane postępowanie może dać błędny wynik. Dlatego pełna praktyczna procedura powinna sprawdzać czy wynik jest poprawny i powtarzać oblicznia w nowymi wartościami y w przeciwnym przypadku. Jednakże prawdopodobiństwo otrzymania błędnego wyniku jest na tyle małe że w rozwiązaniu tego zadania można to pominąć.

Uwaga4. W podobny sposób można obliczać NWD wielomianów więcej niż dwu zmiennych.