Grafomania, a grupa podstawowa
Jedna z najprostszych definicji grafu:
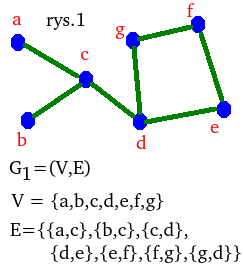
Definicja 1. Parę \((V,E)\) nazywamy grafem o zbiorze wierzchołków \(V\), gdy zbiór jego krawędzi \(E\) jest (pewnym) zbiorem dwuelementowych podzbiorów \(V\).
Definicja 2.
Trasą w grafie \(G=(V,E)\) nazywamy skończony ciąg wierzchołków \(\ll v_0\;v_1\;\ldots\; v_n\rl\) o własności \(\{v_k,v_{k+1}\}\in E\), dla \(k<n\).
Uwaga.
W oznaczeniu ciągu (w trasie) opuściliśmy przecinki z premedytacją - dalej okaże się to wygodne.
Ciąg, w którym jakieś sąsiednie elementy są równe nie jest trasą (dlaczego?).
Tu używana terminologia odbiega nieco od podręcznikowych.
Przykład 3.
W grafie \(G_1\) z rysunku 1.
trasami są np.: \(\ll a\; c\; b\rl\), \(\ll c\; a\; c\; b \rl\),
\(\ll a \;c\; d\; e\; f\; e\; d\rl\), \(\ll c \rl\).
Nie są trasami np.: \(\ll a\; b\; c\rl\), \(\ll a\; d\; e \rl\), \(\ll a\; c\; d\; f\; \rl\), \(\ll c\; c \rl\).
Definicja 4. S-skrócenie trasy, to efekt wielokrotnie stosowanej poniższej operacji:
Gdy w trasie \(\ll v_0\;v_1\;\ldots\;v_{k-1}\;v_k\;v_{k+1}\;\ldots\; v_n\rl\) jest \(v_{k-1}=v_{k+1}\) dla pewnego \(k\), to
opuszczając dwa wyrazy: \(v_k\;v_{k+1}\), otrzymamy S-skrócenie, czyli nową (krótszą) trasę.
Powiemy, że dwie trasy \(\alpha\), \(\beta\) są S-homotopijne (notacja: \(\alpha\sim\beta\)) , gdy istnieje trasa \(\gamma\) będąca ich wspólnym S-skróceniem.
Wy(ob)rażenie. Można sobie wyobrażać: graf \(G\) jest siecią głębokich rowów, wzdłuż trasy układamy sznurek; ciągnąc za końce można spróbować go skrócić ciągle w obrębie grafu (= nie wyciągając z rowów) tak, by otrzymać krótszą trasę (o tym samym początku i końcu) czyli jej S-skrócenie.
Przykład 5. W grafie \(G_1\) z rysunku 1.:
\(\ll a\; c\; b\;c \rl\sim\ll a\; c\; \rl\),
\(\ll a\; c\; d\;c\;a \rl\sim \ll a\; c\; a \rl\sim\ll a \rl\),
\(\ll a \;c\; d\; e\; f\; g\;d\;g\;f\;e\;d\;c\rl \sim \ll a \;c\; d\; e\; f\; g\;f\;e\;d\;c\rl \sim
\ll a \;c\; d\; e\; f\;e\;d\;c\rl \sim \ll a \;c\; d\;c\rl\sim\ll a\;c\rl\),
\(\ll a\; (c\; d)^{2}\;(e\;f)^3\;g\rl=\ll a\; (c\; d)\;(c\; d)\;(e\;f)\;(e\;f)\;(e\;f)\;g\rl\sim \ll a\;c\;d\;e\;f\;g\rl\),
\(\ll a\; (c\; b)^{3}\;c\;d \rl=\ll a\; (c\; b)\;(c\; b)\;(c\; b)\;c\;d \rl\sim \ll a\;c\;d\rl\),
\(\ll a\; (c\; d)^{8}\;(e\;f\;g\;d)^{2}\;c \rl\sim\ll a\; c\;d\; (e\;f\;g\;d)^2\;c) \rl=
\ll a\; c\;(d\;e\;f\;g)^2\;d\;c \rl \).
Definicja 6. Dla grafu \(G=(V,E)\), wierzchołka \(v\in V\) symbol \(\Omega(G,v)\) oznacza zbiór wszystkich tras o początku i końcu w wierzchołku \(v\).
Stwierdzenie \(\bf 7^c\). Dla grafu \(G_1=(V,E)\) z rysunku 1., dla \(k,n\in\mathbb{N}^{+}\) przyjmijmy oznaczenia:
\(\alpha^c=\ll c\rl,\ \ \ \beta^c_k=\ll c\;(d\;e\;f\;g)^k\;d\;c \rl, \ \ \ \gamma_n^c=\ll c\;(d\;g\;f\;e)^n\;d\;c \rl.\)
Mamy:
\((i)\) \(\alpha^c, \beta_k^c, \gamma_n^c\) są S-nieskracalne,
\((ii)\) każde dwie różne spośród tras \(\alpha^c, \beta_k^c, \gamma_n^c\) nie są S-homotopijne,
\((iii)\) każda trasa \(\omega\in \Omega(G_1,c)\) jest S-homotopijna z którąś z tras: \(\alpha^c, \beta_k^c, \gamma_n^c\) .
Zadanie \(\bf 7^b\). Dla grafu \(G_1=(V,E)\) z rysunku 1, wskaż analogiczne trasy jak w Stwierdzeniu \(7^c\), gdzie rolę wierzchołka \(c\) będzie pełnić wierzchołek \(b\).
Zadanie \(\bf 7^e\). Dla grafu \(G_1=(V,E)\) z rysunku 1, wskaż analogiczne trasy jak w Stwierdzeniu \( 7^c\), gdzie rolę wierzchołka \(c\) będzie pełnić wierzchołek \(e\).
Definicja 8.
Dla dwóch tras \(\varphi=\ll u_0\;u_1\;\ldots\; u_n\rl\), \(\psi=\ll v _0\;v_1\;\ldots\; v_k\rl\) takich, że \(u_n=v_0\) określamy iloczyn tych tras jako trasę \(\varphi\star\psi=\ll u_0\;u_1\;\ldots\; u_n\;v_1\;\ldots\; v_k\rl\) .
Niech dla \(\varphi=\ll u_0\;u_1\;\ldots\;u_{n-1}\; u_n\rl\) będzie \(\phi^{-1}=\ll u_{n}\;u_{n-1}\;\ldots\;u_1\; u_0\rl\), czyli \(\varphi\) zapisane wspak.
(Uwaga. Na ogół nie może być nawet mowy o przemienności działania \(\star\); dlaczego?)
Przykład 9. W grafie \(G_1\) z rysunku 1. ograniczmy się do tras z \(\Omega(G_1,c)\):
\(\ll c\; b\;c\;a\;c \rl \star \ll c\; d\; e\;d\;c\rl \sim \ll c\rl\),
\(\ll c\; (d\;e\;f\;g)^2 \;d\;c\rl \star \ll c\; (d\;e\;f\;g)^3 \;d\;c\rl \sim \ll c\; (d\;e\;f\;g)^5 \;d\;c\rl\),
Dla dowolnego \(\varphi\in \Omega(G_1,c)\) mamy: \(\ \varphi\star \ll c\rl = \ll c\rl \star \varphi =\varphi,\ \)
\(\ \varphi\star \varphi^{-1}\sim \ll c\rl \sim \varphi^{-1}\star \varphi\).
Dla \(\ \beta_k=\ll c\;(d\;e\;f\;g)^k\;d\;c \rl, \ \gamma_n=\ll c\;(d\;g\;f\;e)^n\;d\;c \rl\) mamy dla liczb całkowitych \(k,m\in\mathbb{Z}\):
\(\beta_1^{-1}\star \gamma_1\sim \ll c\rl, \)
\(\beta_k\sim\beta_1^k, \)
\(\gamma_k\sim\gamma_1^k, \)
\(\beta_k \star \beta_m\sim \beta_{k+m}\sim (\beta_1)^k \star (\beta_1)^m , \)
\(\gamma_k \star \gamma_m\sim \gamma_{k+m}\sim (\gamma_1)^k \star (\gamma_1)^m\),
\(\beta_1^{0}\sim \ll c\rl \sim \gamma_m^0, \)
Stwierdzenie \(\bf 10^c\). Dla grafu \(G_1\) z rys. 1., dla \(\beta=\ll c\;d\;e\;f\;g\;d\;c \rl\)
mamy:
\((a)\) \(\beta^m\star \beta^n\sim \beta^{m+n}\) dla każdego \(m.n\in\mathbb{Z}\),
\((b)\) dla każdej trasy \(\omega\in \Omega(G_1,c)\) istnieje dokładnie jedno \(k\in\mathbb{Z}\) takie, że
\(\omega\sim \beta^k\),
\((c)\) zbiór ilorazowy \(\Omega(G_1,c)/_{\sim}\) z działaniem \(\star\) jest izomorficzny z grupą \((\mathbb{Z},+)\) .
Zauważmy, że dla \( \ll e\;d\;c \rl\star (\ll c\;d\;e\;f\;g\;d\;c \rl)^k\star (\ll e\;d\;c \rl)^{-1} \in \Omega(G_1,e)\).
Ta obserwacja pozwala dowieść, że
Stwierdzenie \(\bf 11\). Dla grafu \(G_1\) z rys.1, dowolnego \(v\in V\)
i dowolnej trasy \(\delta=\ll v\;\ldots\;c\rl\) z \(v\) do \(c\) mamy:
\((a)\) \(
\delta\star\varphi\star \delta^{-1} \sim \delta\star\varphi'\star \delta^{-1}
\iff \varphi \sim \varphi'
\ \) dla każdych tras \(\ \varphi,\varphi'\in \Omega(G_1,c)\),
\((b)\) \(
\delta^{-1}\star\psi\star \delta \sim \delta^{-1}\star\psi'\star \delta
\iff \psi \sim \psi'
\ \) dla każdych tras \(\ \psi,\psi'\in \Omega(G_1,v)\),
\((c)\) zbiory ilorazowe \(\Omega(G_1,c)/_{\sim}\), \(\Omega(G_1,v)/_{\sim}\) z działaniem \(\star\) są izomorficzne,
\((d)\) zbiór ilorazowy \(\Omega(G_1,v)/_{\sim}\) z działaniem \(\star\) jest izomorficzny z grupą \((\mathbb{Z},+)\) .
A jak to wszystko się ma do grupy postawowej?
\(\bullet\) Wierzchołki grafu utożsamiamy z punktami z \(\mathbb{R}^n\) (wystarczy \(n=3\)) tak położonymi, by żadne 4 nie leżały w jednej płaszczyźnie.
\(\bullet\) Krawędź \(\{u,v\}\) grafu utożsamiamy z odcinkiem \(uv=\{(1-t)u+tv: t\in[0,1]\}\).
\(\bullet\) Suma takich odcinków i punktów tworzy realizacją geometryczną \(\hat{G}\) grafu \(G\).
\(\bullet\) Trasę \(\varphi=\ll v_0\;v_1\;\ldots\; v_n\rl\) utożsamiamy z funkcją
\(\hat{\varphi}:[0,1]\to \hat{G}\) określoną wzorem:
\(\hat{\varphi}({k \over n})=v_k\), dla \(k\in\{0,1,\ldots n\}\), a na reszcie - liniowo, to znaczy:
\(\hat{\varphi}(x)= n({k+1\over n}\!-\!x)v_k+n(x\!-\!{k\over n})v_{k+1} \) gdy \(x\in[{k\over n},{k+1\over n}].\)
Dla trasy \(\varphi=\ll v_0\rl\) musimy (niestety) zdefiniować ją oddzielnie, jako funkcję stałą
\(\hat{\varphi}(x)= v_0\).
\(\bullet\) Iloczynowi \(\varphi\star\psi\) tras \(\varphi,\psi\in \Omega(G,v)\) odpowiada iloczyn pętli \(\hat{\varphi}\star\hat{\psi}\).
\(\bullet\) Nieco kłopotliwy (technicznie) jest opis uzasadnienia, że
jeśli \(\varphi\sim\psi\) są S-homotopijne
w \(G,\) to \(\hat{\varphi}\sim\hat{\psi}\), czyli \(\hat{\varphi},\hat{\psi}\) są homotopijne w \(\hat{G}\).
Pomysł polega na zapisaniu formułami owego skracania sznurka (opisanego powyżej w Wy(ob)rażeniu).
"Wolno ciągnąc za końce sznurka, położenie sznurka będzie się zmieniać nieznacznie", czyli w sposób ciągły; oto idea owej homotopii. Pomijamy szczegóły; można zaglądnąć do tekstu: Zobaczmy dwie homotopijne pętle, gdzie jest ilustracja przykładu takiej homotopii.
\(\bullet\) Wydaje się dużo, dużo trudniejsze pokazanie, że w grafie spójnym:
każda pętla \(p\in\Omega(\hat{G},v)\) jest homotopijna z pętlą \(\hat{\varphi}\) powstałą z pewnej trasy \(\varphi\in \Omega(G,v)\).
Bowiem bogactwo funkcji ciągłych jest dużo, dużo większe niż tras w grafie. Jednak jest twierdzenie: bliskie funkcje w 'ładne' przestrzenie są homotopijne. (Tu ładne oznacza ANR; realizacje grafów są takie.) Pomijamy szczegóły.
\(\bullet\) Wszystko to, co powżej pozwala uzasadnić:
Grupa podstawowa \(\Omega(\hat{G_1},v)/_{\sim}\) jest izomorficzna ze
grupą \(\Omega(G_1,v)/_{\sim}\), czyli z \((\mathbb{Z},+)\).
\(\bullet\) Ogólnie, dla realizacji geometrycznych grafów spójnych, grupa podstawowa może być badana tak samo. Jednak w nieco tylko bardziej skomplikowanych grafach grupy te są dużo bogatsze.
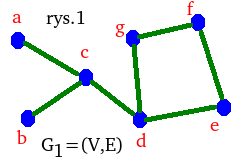
Zadanie łatwe.
Znaleźć grupę podstawową realizacji \(\hat{G_2}\) grafu \(G_2\) z rysunku obok.
Wskazówka.
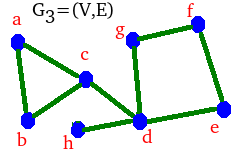Zadanie trudne.
Znaleźć grupę podstawową realizacji \(\hat{G_3}\) grafu \(G_3\) z rysunku obok.
Wskazówka 0.
Wskazówka 1.
Wskazówka 2.
Wskazówka 3.