Excel

$\ \ \ \bullet$ 1. (26.02.2025) Adresy obszarów z/bez dolarów

Zapisz poniższe pliki u Siebie:
1.1 25_1rytmy.ods
1.2 25_1zakupy.ods
1.3 25_1dzienn1.ods
1.4 25_1deska.ods
1.5 25_1place.ods

Niech $m\in\NN, m\geq 2$ będzie ustalone. Dla liczb naturalnych $k,n,\ n>k>0,$ definiujemy:
       ${n\choose 0}_m=1,\ $ ${n\choose n}_m=1,\ \ $ ${n \choose k}_m = {n-1 \choose k-1}_m \oplus {n-1\choose k}_m $,
gdzie $\oplus$ oznacza dodawanie modulo $m$.

  Zmuś arkusz kalkulacyjny, by wyświetlił:
  1.6 kilkanaście początkowych wierszy trójkąta Pascala$_m$, dla $m=99$,
  1.7 kilkadziesiąt początkowych wierszy trójkąta Pascala$_m$, dla $m=2$,
  1.8 kilkadziesiąt początkowych wierszy trójkąta Pascala$_m$, dla $m=3$,
  1.9 kilkadziesiąt początkowych wierszy trójkąta Pascala$_m$, dla $m=4$.
  CO WIDAĆ? (Wyłącz [narzędzia][opcje][LibreOffice Calc][Widok][watości zerowe])

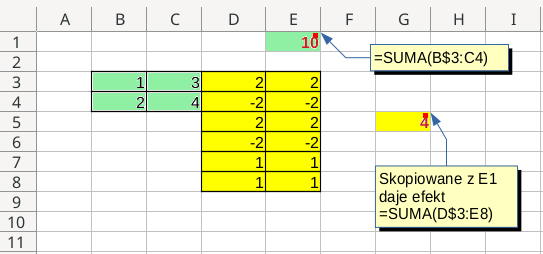
ZApamiętaj: nie dolaruj na daremno!

$\ \ \ \bullet$ 2. (05.03.2025)

  2.1 Zapisz i wypełnij plik: 25_2konkurs.ods

  2.2 a) Zrób tabliczkę mnożenia $12\times 12$:
        -- wypełnij pierwszy wiersz i pierwszą kolumnę
        -- wypełnij JEDNO z pozostałych pól tabliczki TAK, BY po skopiowaniu do pozostałych otrzymać resztę tabliczki

  2.2 b) Dla każdego $m\in\NN, m\leq 12$ oblicz sumę liczb tabliczki mnożenia $m\times m$.    (GDZIE umieścić wyniki?)

  2.2 c) Zrób tabliczkę $\oplus$-dodawania modulo $m$. Jaka jest suma modulo $m$ liczb takiej tabeliczki?

  2.2 d) Zrób tabliczkę $\odot$-mnożenia modulo $m$. Jaka jest suma modulo $m$ liczb takiej tabeliczki?

  2.3 Zapisz i wypełnij plik: 25_1deska.ods (o ile jeszcze nie zrobiłeś)

  2.4 Definiujemy synbol ${n\choose k}_T$ dla liczb naturalnych $k,n,\ 0\leq k\leq n$ :
       $\ \ \ {n\choose 0}_T=1,\ $ ${n\choose n}_T=1\ \ $ oraz $\ \ {n \choose k}_T = {n-1 \choose k-1}_T + {n-2\choose k-1}_T+ {n-1\choose k}_T \ \ $ dla $n>k\geq 1$.

  Zmuś arkusz kalkulacyjny, by wyświetlił kilkanaście początkowych wierszy trójkąta T.
  CO WIDAĆ?

  2.5 Zapisz i wypełnij plik: 25_2skoki.ods

$\ \ \ \bullet$ 3. (12.03.2025) SUMA.JEŻELI, LICZ.JEŻELI, INDEKS, WYSZUKAJ.PIONOWO, PODAJ.POZYCJĘ

  3.2 Zapisz u Siebie plik: 25_3Europa.csv, otwórz go w arkuszu i zapisz w formacie *.ods

  3.2 a) Nazwij kolumny ([Wstaw][Definiuj...]); zrób podsumowanie (kolumn)

  3.2 b) Znajdź odpowiedzi:
        (i) Ile państw ma większą powierzchnię od Polski?
        (ii) Ile ludzi żyje w państwach mniej licznych niż Polska?
        (iii) Ile państw ma mniej ludności od Polski?
        (iv) Ile państw ma większą niż Polska gęstość zaludnienia?

  3.2 c) Dodaj kolumny rankingów ( $1 <\!\sim\! >$ największe):
        (i) wg liczby mieszkańców
        (ii) wg powierzchni
        (iii) wg gęstości zaludnienia

  3.2 d) Znajdź odpowiedzi:
        (i) Znajdź państwa, w których: liczba ludności /powierzchnia/ jest równa /odpowiedniej/ medianie?
        (ii) Ile ludzi żyje w państwach o większej gęstości zaludnienia niż ma Polska?

  3.3 W pliku-dzienniku dodaj (w 'rozsądnych' miejscach):

  3.3 a) rozkłady ocen poszczególnych uczniów (tzn. ile 2 ma Jaś, ile 3 ma Jaś ,...)
        (i) poszczególnych uczniów (tzn. ile 2 ma Jaś, ile 3 ma Jaś ,...),
        (ii) poszczególnych przedmiotów.
        (iii) GDZIE umieścić rozkład ocen CAŁEJ klasy?

  3.3 b) ranking wg średniej ocen.

  3.3 c) (niemal) kopię tabeli ocen posortowaną (DYNAMICZNIE) wg średniej ocen.


  3.4 Zapisz i wypełnij plik: 25_2skoki.ods (o ile jeszcze nie zrobiłeś)

$\ \ \ \bullet$ 5. (26.03.2025) funkcje tablicowe (CSE = Control+Shit+Enter)

  5.1 Zapisz i wypełnij plik: 25_5f_tabl_przyklady1.ods

  5.2 Zapisz i wypełnij plik: 25_5uklad_Gauss.ods

  5.3 Zapisz i wypełnij plik: 25_5uklad_inv.ods

$\ \ \ \bullet$ 9. (30.04.2025)

9.1 Zapisz plik: dz_ocen.txt

9.2 Zapisz plik: dz_frek.txt

$\ \ \ \bullet$ 12. (21.05.2025)

  Plany: źródła (poprzednie):
           25_10planALL.csv
           25_10planPRZEDM.csv
           25_10planOSOB.csv

  Zapisy (rejestracje) na zajęcia źródło:
           25_plan_zapisy.csv (uwaga: nie są to rzeczywiste dane)

  1. Poniżej są typowe pytania związane z zapisami; znajdź odpowiedzi.
      1 a) Ile osób zapisało się na poszczególne przedmioty?
      1 b) Ile osób zapisało się do poszczególnych grup?
      1 c) Na których laboratoriach przekroczony jest limit 15 osób?
      1 d) W których grupach jest mniej niż 10 osób?
      1 e) Którzy studenci wybrali więcej niż 7 przedmiotów?

  2. Zapisy mogą zawierać błędy. JAKIE?
      2 a) Jest możliwe wiele rodzajów błędów. Sformułuj ('na sucho') kilka różnych typów/rodzajów.
      2 b) Niektóre można sprawdzić przy tych danych. Zrób to.

  3*. Jak zobaczyć różne kolizje w planach poszczególnych studentów?
      Czy można zrobić wielgachną JEDNĄ tabelę zwierającą wszystkie dane z czterech plików (zapisy + trzy wcześniejsze)?

$\ \ \ \bullet$ 13. (28.05.2025)

  Plany:
           25_10planALL.csv
    W Excelu jak i w LibreOfficeCalc tabela przestawna 'nie daje sobie rady' z natępującymi pytaniami
     (A) Na ile przedmiotów zapisał się dany student?
     (B) Ilu studentów zapisało się na dany przedmiot?

     Bowiem funkcje zlicz (COUNT) liczą liczbę WSZYSTKICH rekordów.
     BRAK jest funkcji agregującej DISTINCT COUNT (inna nazwa: COUNTUNIQUE).

    Rozwiązania:
     Wybrać z danych tylko dwie kolumny: student i id_przed, po czym usunąć powtarzające się rekordy (poszukać w opcjach GRUPUJ)
     ALBO
     znaleźć lepszy (pod tym względem) arkusz kalkulacyjny, np.: GoogleArkusz ALBO https://rows.com/
     ALBO
     do danych dodać nową kolumnę, która pokażę (wartość 1) tylko pierwsze wystąpienia danej pary: student-id_przed
     co zilustrowano w pliku    25_plan_zapisy_roz.ods

$\ \ \ \bullet$ 15. (11.06.2025)

Ja ci pokażę, jak wilk goni zająca i krzyczy:
    'Ja ci pokażę! Jak wilk goni zająca i krzyczy:
       'Ja ci pokażę! Jak wilk goni zająca i krzyczy:
          'Ja ci pokażę! Jak wilk goni zająca i krzyczy:
             'Ja ci pokażę! Jak wilk goni zająca i krzyczy:
                        $\vdots$

Wilk i zając (bajka, tylko dla dorosłych)
Dawno, dawno temu, wilk i zając byli na zielonej łące.
Na początku w punktach $W_1=(-1,2)$ i $Z_1=(3,0)$.
Nie zważając na nic zając zaczął skakać w koło (a dokładniej po okręgu o środku $(0,0)$ i promieniu $R=3$).
Co sekundę był już dalej i dalej: $Z_1,\;Z_2,\;Z_3,\;Z_4,\ldots $; tak dobierał długość susów, by $Z_{91}=Z_1,\;Z_{92}=Z_2,\;Z_{93}=Z_3,\ldots$
i dalej już skakał po własnych śladach.
Co na to wilk? Krzyczy 'Ja ci pokażę!' i...
od razu podjął zabawę: ruszył za zającem też skacząc: $W_1,\;W_2,\;W_3,\;W_4,\ldots $ (skacząc? Tak, przecież to... bajka!)
przy czym STALE kierował się na zająca, to znaczy:
Gdy wilk w chwili $j$ jest w $W_j$, to widzi zająca w $Z_j$ i skacze tak, że $W_{j+1}$ leży na półprostej $W_jZ_j{\vec{\ }}$,
przy czym długość skoku wilka jest połową długości (aktualnego) skoku zająca.

Powyższe można streścić tak: $\ \ \overrightarrow{W_jW_{j+1}} = s\cdot { || \overrightarrow{Z_jZ_{j+1}}|| \over|| \overrightarrow{W_jZ_{j}} ||}\cdot \overrightarrow{W_jZ_{j}},\ \ \ \ $ gdzie $\ s=\frac{1}{2}\ $ oraz $\ j=1,2,3,\ldots$.

Jak skończyła się ta historia? To nie jakaś tam historyjka, to jest BAJKA, nigdy się nie kończy!

Zmuś arkusz kalkulacyjny, by Ci pokazał wszystkie punkty $\ W_j,\;Z_j\ $ dla $j\leq n=300$.
CO widać???

Uwaga: Co się dzieje, gdy kiedyś przypadkiem się spotkają?
NIC STRASZNEGO! Kłaniają się sobie nawzajem i ruszają dalej! (Straszne są tylko bajki dla dzieci.)
Ciekawsze jest pytanie:
Czy - zmieniając pozycje $W_1,\;Z_1$ - może się tak zdarzyć, że wpadną na siebie?